เฉลยให้ก่อนนะ
Q-1803
ถ้า z
1, z
2 เป็นรากของสมการ (z - 2
)
3 = -8i
ซึ่งมีขนาดเป็น
จำนวนเต็ม แล้ว z
1 + z
2 เท่ากับข้อใดต่อไปนี้
จะเปลี่ยน -8i ให้อยู่ในรูปเชิงขั้วได้
-8i = 0 - 8i
ดังนั้น r =
= 8
และ tan
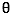
=
=
ซึ่งจะตรงกับ
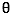
= 270

ตรงนี้รู้ว่า 270

ดูจากแกนส่วนจริง ส่วนจินตภาพก็ได้ค่ะ
ดังนั้น -8i = 8(cos 270 + i sin270
+ i sin270 )
)
จาก
(z - 2
)
3 = 8(cos 270

+ i sin270

)
จะถอด
รากที่สาม เข้าสูตรถอด
รากที่สามของ
จำนวนเชิงซ้อนค่ะ
( (z - 2
)
3 )
= r
[ cos
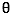 +2k +2k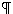 |
| n |
+ i sin
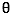 +2k +2k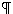 |
| n |
]
เมื่อ k = 0,1,2
จะได้ ออกมา 3 ค่า
ถ้า k = 0
z - 2
= 8
[ cos
270 |
| 3 |
+ i sin
270 |
| 3 |
]
z - 2
=2( cos90

+ i sin90

)
z - 2
= 2(0 + i(1))
z - 2
= 2i
z = 2
+ 2i
ซึ่ง |z| =
=
=
= 4 ได้เป็น
จำนวนเต็ม
แปลว่า z = 2 + 2i ใช้ได้ เก็บไว้ก่อน
ถ้า k = 1 แทนค่าแบบข้างบนเลย จะได้
z - 2
=2( cos210

+ i sin210

)
z - 2
= 2 (-
-
i )
z - 2
= -
- i
z = -
- i + 2
z =
- i
ซึ่ง |z| =
=
= 2
แปลว่า z = - i ใช้ได้ เก็บไว้ก่อน
ถ้า k = 2
แทนแบบเดิม ทำแบบเดิม ทำนองเดียวกัน
แต่ว่า |z| ที่ได้ จะไม่เป็นจำนวนเต็มค่ะ ค่า z ตัวนี้เลยใช้ไม่ได้
สรุป z1, z2 ที่โจทย์หมายถึงก็คือ
2
+ 2i กับ
- i
โจทย์ถามผลบวก
= 2
+ 2i +
- i
= 3
+ i
ตอบค่ะ